Hyperplane at infinity

In mathematics, in particular projective geometry, the hyperplane at infinity, also called the ideal hyperplane, is an (n−1)-dimensional projective space added to an n-dimensional affine space A, such as the real affine n-space 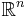\mathbb{R}^n , in order to obtain uniformity of incidence properties. Adding the points of this hyperplane (called ideal points or points at infinity) converts the affine space into an n-dimensional projective space, such as the real projective space 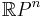\mathbb{R}P^n. There is one ideal point added for each pair of opposite directions in A.

By adding these ideal points, the entire affine space A is completed to a projective space P, which may be called the projective completion of A. Each affine subspace S of A is completed to a projective subspace of P by adding to S all the ideal points corresponding to the directions of the lines contained in S. The resulting projective subspaces are often called affine subspaces of the projective space P, as opposed to the infinite or ideal subspaces, which are the subspaces of the hyperplane at infinity (however, they are projective spaces, not affine spaces).

In the projective space, each projective subspace of dimension k intersects the ideal hyperplane in a projective subspace "at infinity" whose dimension is k − 1.

A pair of non-parallel affine hyperplanes intersect at an affine subspace of dimension n − 2, but a parallel pair of affine hyperplanes intersect at a projective subspace of the ideal hyperplane (the intersection lies on the ideal hyperplane). Thus, parallel hyperplanes, which did not meet in the affine space, intersect in the projective completion due to the addition of the hyperplane at infinity.

Similarly, parallel lines intersect at the point at infinity which corresponds to their common direction.

In a projective space, any hyperplane may be chosen to be the hyperplane at infinity. Specifically, if P is a projective space and H is a hyperplane of P, then P − H is an affine space whose projective completion is P. Thus, the ideal hyperplane cannot be identified in terms of P alone.

See also

References